Math

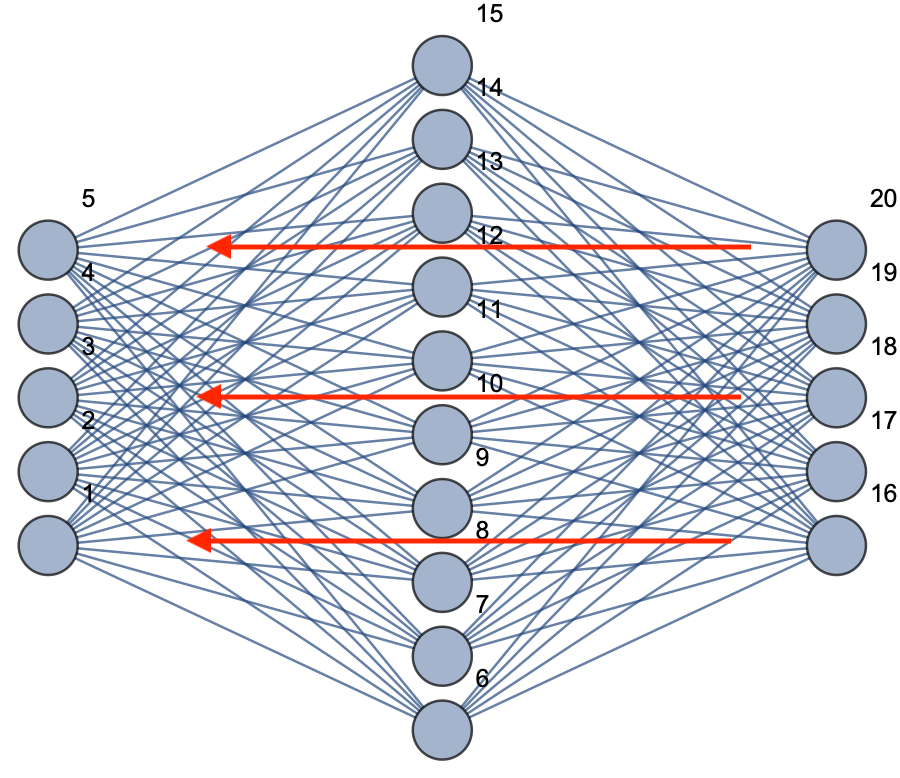
关于人工神经网络 人工神经网络模型判断手写数字 我们首先在Mathematica中徒手打造一个人工神经网络，然后对该神经网络进行训练，最后用训练得到的模型来判断图片上的手写数字是多少。 trainingData = ResourceData["MNIST", "TrainingData"]; testData = ResourceData["MNIST", "TestData"]; net = NetInitialize@NetChain[{ FlattenLayer[], LinearLayer[500], ElementwiseLayer["Sigmoid"], LinearLayer[100], ElementwiseLayer["Sigmoid"], LinearLayer[10], SoftmaxLayer[]}, "Input" -> NetEncoder[{"Image", {12, 12}, "ColorSpace" -> "Grayscale"}], "Output" -> NetDecoder[{"Class", Range[0, 9]}]] NetEncoder告诉我们输入的单通道12*12的图像 NetDecoder告诉我们我们的神经网络模型最后输出的是一个分类，类别分别是0-9中的一个数字 网络层的模型为： FlattenLayer[] 图像中的像素数据即两纬数据排列成一纬数据做为输入 LinearLayer[500] 第一层线性层，输出数据为500个，限定函数为Sigmoid LinearLayer[100] 第二层线性层，输出数据为100个，限定函数为Sigmoid LinearLayer[10] 最后一层输出，因为我们需要有10个分类，所以这里设定是10，限定函数为 Softmax 神经网络层形象的展示如下: 训练数据标记，左边是实际的手写数字，右边是对应标签 RandomSample[trainingData, 10] 在未对模型进行训练前，使用随机的权重来判断图片，我们可以确定错误率接近100% 对模型进行训练 trained = NetTrain[net, trainingData, ValidationSet -> testData, MaxTrainingRounds -> 50 ] 从以上图表中我们大致可以看出正确率已经接近97% 再次预测上述图片，模型已经可以正确预测给出的图片数字为6 measurements = ClassifierMeasurements[trained, testData] 运行 measurements[“Accuracy”] 我们可以得到模型的正确率为98.02% ...

SIR Modeling The SIR classical model is mainly used in the field of infectious diseases to predict future trends in the number of infections. S[t] denotes susceptible susceptible population I[t] denotes infected population already infected R[t] indicates recovered recovered population Reference: MathWorld: SIR Model Kermack-McKendrick Model Kermack-McKendrick Model The original Kermack-McKendrick model was designed to account for changes in the number of people infected over time, like the plague that occurred in 1665-1666 and the cholera that occurred in 1865. The model assumes that the total population is fixed, that the incubation period for infectious diseases is instantaneous, that the duration of infection is the same as the disease cycle, and that the population is assumed to be non-differentiable, without differences by gender or race. ...

Lotka Volterra 方程 维基百科解释: Lotka Volterra 该方程组描述了 捕食系统模型 微分方程为: dx/dt = Axy - Bx dy/dt = Cy - Dxy => dy/dx = (Cy - Dxy) / (Axy - Bx) (1.1) {A, B, C, D} 均为模型系数 对微分方程(1.1)求解为: W 为Lambert W function 当系数为 {A -> 0.1, B -> 2, C -> 4, D -> 0.4, x -> {1,30}} y[x] 由于我们需要获得 x,y 关于自变量时间t，在模型系数{A,B,C,D}下的模型图，所以在Mathematica中对该方程组定义和设置模型系数 求该方程的数值解 创建Modelica模型 在0时刻 x[0] = 10, y[0] = 5 model = CreateSystemMod["Hare", Join[predatorPreyEq, {x[0] == 10, y[0] == 5}], t, Association[{"ParameterValues" -> params}]] 建模 Modelica 模型源码 ...

Why study Modelica I have seen a book “Model Thinking” before, and this time it happens to be in the CoVid-2019 disease ravaging the world, by chance I saw the prediction model SEIR about epidemiology, I took this opportunity to start studying mathematical models, and decided to pick up the mathematical analysis, ordinary differential equations, partial differential equations, differential geometry and other courses I studied in college. I came across the language Modelica, and since I had been studying Wolfram Mathematica, I was quite fond of SystemModeler of the Wolfram product line, so I started to buy the home edition of SystemModeler and purchased a book “Introduction and Improvement of Modelica Multi-Domain Physical System Modeling”. I began my exploration of Modelica with the expectation of gaining a deeper understanding of mathematical model building, using mathematical models to predict the future development pattern of an event and gaining more hidden information in quantitative data analysis. ...