SIR Modeling

The SIR classical model is mainly used in the field of infectious diseases to predict future trends in the number of infections.

S[t] denotes susceptible susceptible population

I[t] denotes infected population already infected

R[t] indicates recovered recovered population

Reference:

MathWorld:

• SIR Model
• Kermack-McKendrick Model

Kermack-McKendrick Model

The original Kermack-McKendrick model was designed to account for changes in the number of people infected over time, like the plague that occurred in 1665-1666 and the cholera that occurred in 1865. The model assumes that the total population is fixed, that the incubation period for infectious diseases is instantaneous, that the duration of infection is the same as the disease cycle, and that the population is assumed to be non-differentiable, without differences by gender or race.

The model uses three nonlinear ordinary differential equations:

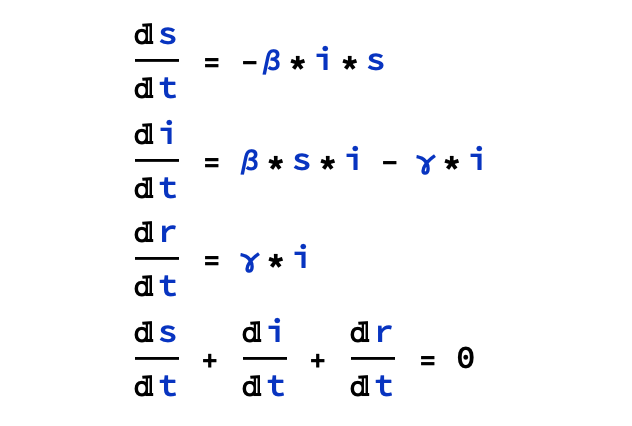
• beta denotes infection rate infection rate
• gamma denotes recovery rate recovery rate
• i indicates infected population
• r indicates recovered population
• s indicates susceptible population

Pre-set values: beta = 20%, gamma = 15%, i(0) = 0.1, r(0) = 0, s[0] = 10

Modelica source code

model model SIRModel parameter Real beta = 0.2; parameter Real gamma = 0.15; Real i; Real r; Real s; initial equation s = 10; i = 0.1; r = 0; equation der(s) = (-1) * beta * i * s; der(i) = (-1) * gamma * i + beta * i * s. der(i) = (-1) * gamma * i + beta * i * s; der(r) = gamma * i; end SIRModel;

Model prediction graph:

![SIRModelPlot](/images/mathematica/SIRModelPlot.png)

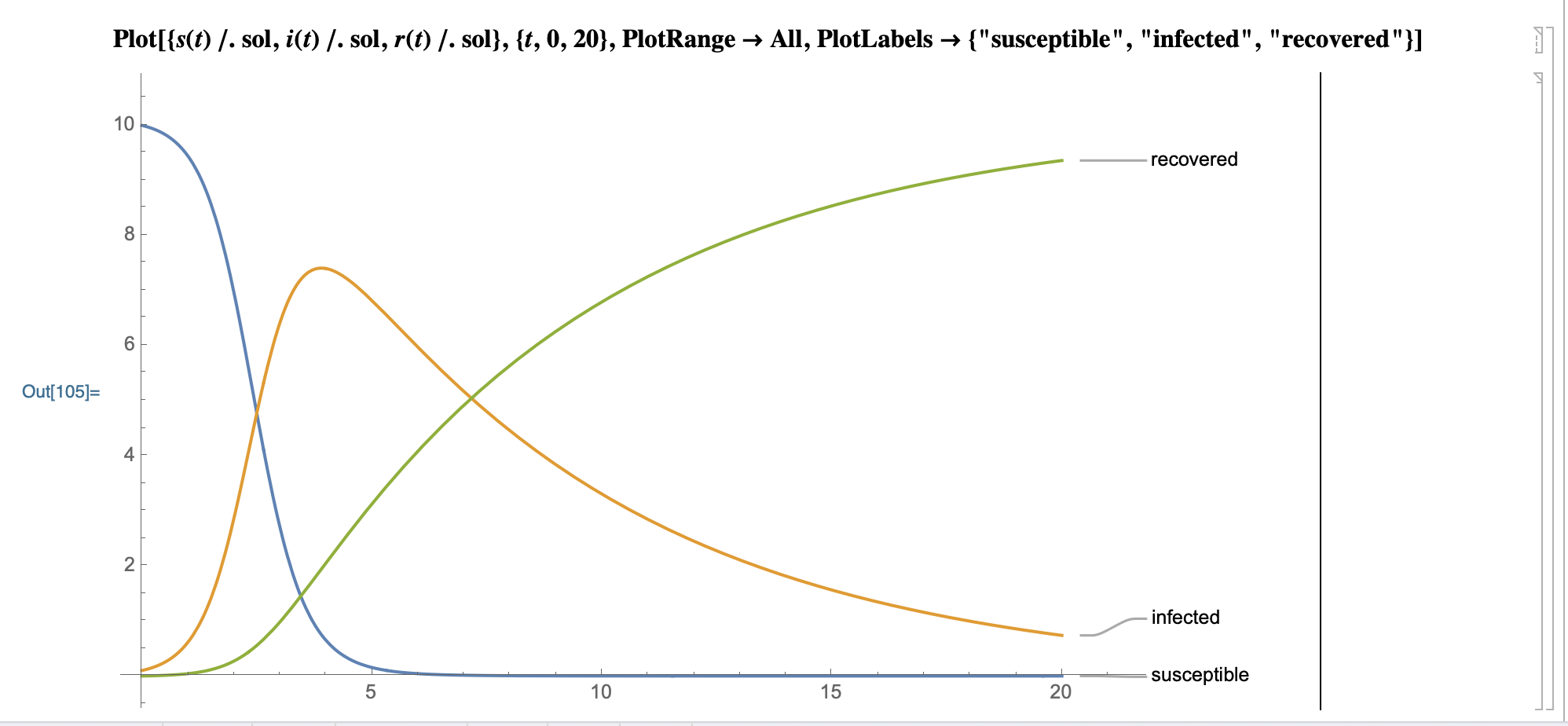
SystemModeler prediction plot

![SIRModelPlot2](/images/mathematica/SIRModelPlot2.png)



## SEIR Model ##

Doing