Blogs

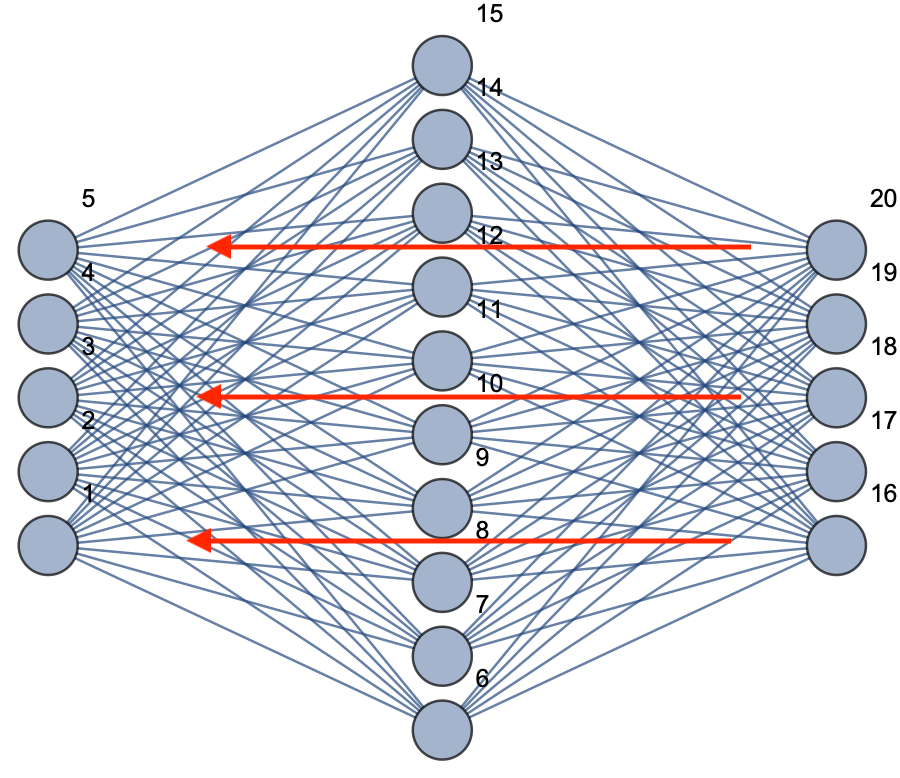
Convolutional neural networks About convolution can be abstracted into mathematical expressions: I can represent the matrix of an image, K is the convolution kernel The computational layer of the convolution Object Recogition with Gradient-Based Learning input layer Input Layer Convolution Layer Conv Layer Restricted Layer RELU Layer pooling layer Pooling Layer full connected layer Creating a network Basic learning to distinguish between dogs and cats (* Create model *) myCatDogModel = NetChain[{ ConvolutionLayer[32, 3], Ramp, PoolingLayer[2, 2], ConvolutionLayer[64, 3], Ramp, PoolingLayer[2, 2], FlattenLayer[], 128, Ramp, 2, SoftmaxLayer[]}, "Input" -> NetEncoder[{"Image", {224, 224}, ColorSpace -> "RGB"}] , "Output" -> NetDecoder[{"Class", {"cat", "dog"}}]] (* Collect samples, training set and test set *) (* Convert data sets to Association format *) dataSetsConvert[dateSets_] := Module[ {}, File[#] -> StringSplit[FileBaseName[#], "."] [[1]] & /@ dateSets] traingDataFiles = RandomSample[dataSetsConvert[traingData]]; testDataFiles = RandomSample[dataSetsConvert[testData]]; SetDirectory[ "/Users/alexchen/datasets/Convolutional_Neural_Networks/dataset"]; FileNames["*.jpg", "training_set/cats/"]; FileNames["*.jpg", "training_set/dogs/"]; traingData = Join[FileNames["*.jpg", "training_set/cats/"], FileNames["*.jpg", "training_set/dogs/"]]; testData = Join[FileNames["*.jpg", "test_set/cats"], FileNames["*.jpg", "test_set/dogs"]]; (* Generate training and validation sets *) traingDataFiles = RandomSample[dataSetsConvert[traingData]]; testDataFiles = RandomSample[dataSetsConvert[testData]]; (* sample is randomly selected for display *) RandomSample[traingDataFiles, 5] (* train the model *) mytrainedModel = NetTrain[catdogModel, traingDataFiles, All, ValidationSet -> testDataFiles, MaxTrainingRounds -> 20] (* Generate training model evaluation report *) myModelPlot = mytrainedModel["FinalPlots"] (* Generate the trained model to calculate the model correctness *) myTrainedNet = mytrainedModel["TrainedNet"] ClassifierMeasurements[myTrainedNet, testDataFiles, "Accuracy"] ...

蛋白质的组成 蛋白质基本上就是一部分子机器，对生命的支撑起着关键作用。 蛋白质属于高分子聚合物，是由氨基酸残基组成的多肽链。 蛋白质在工作过程中，它的三维结构即多肽链的结构是以严格确定的方式折叠起来的。 蛋白质折叠结构中分为 一级 -> 四级 结构 组成多肽链的氨基酸序列决定了蛋白质的三维结构，即蛋白质的一级结构决定了蛋白质的三维结构 蛋白质的生产过程 蛋白质的基本组成单位 - 氨基酸 氨基酸的维基百科 基本的20种氨基酸名称结构和表达式: 氨基酸的基本结构: 可以分为 氨基(NH2)，羧基(CO2H)，侧链(R) 蛋白质构象 Rosetta 蛋白质折叠

开启 Hello AI World 之旅 官方项目的源码地址 jetson nano 硬件配置 GPU架构: 128-core Maxwell CPU: Quad-core ARM A57 @ 1.43 GHz Memory: 4 GB 64-bit LPDDR4 25.6 GB/s Storage: microSD Card Video Encode: 4K @ 30 | 4x 1080p @ 30 | 9x 720p @ 30 (H.264/H.265) Video Decode: 4K @ 60 | 2x 4K @ 30 | 8x 1080p @ 30 | 18x 720p @ 30 (H.264/H.265) Camera: 2x MIPI CSI-2 DPHY lanes ...

关于人工神经网络 人工神经网络模型判断手写数字 我们首先在Mathematica中徒手打造一个人工神经网络，然后对该神经网络进行训练，最后用训练得到的模型来判断图片上的手写数字是多少。 trainingData = ResourceData["MNIST", "TrainingData"]; testData = ResourceData["MNIST", "TestData"]; net = NetInitialize@NetChain[{ FlattenLayer[], LinearLayer[500], ElementwiseLayer["Sigmoid"], LinearLayer[100], ElementwiseLayer["Sigmoid"], LinearLayer[10], SoftmaxLayer[]}, "Input" -> NetEncoder[{"Image", {12, 12}, "ColorSpace" -> "Grayscale"}], "Output" -> NetDecoder[{"Class", Range[0, 9]}]] NetEncoder告诉我们输入的单通道12*12的图像 NetDecoder告诉我们我们的神经网络模型最后输出的是一个分类，类别分别是0-9中的一个数字 网络层的模型为： FlattenLayer[] 图像中的像素数据即两纬数据排列成一纬数据做为输入 LinearLayer[500] 第一层线性层，输出数据为500个，限定函数为Sigmoid LinearLayer[100] 第二层线性层，输出数据为100个，限定函数为Sigmoid LinearLayer[10] 最后一层输出，因为我们需要有10个分类，所以这里设定是10，限定函数为 Softmax 神经网络层形象的展示如下: 训练数据标记，左边是实际的手写数字，右边是对应标签 RandomSample[trainingData, 10] 在未对模型进行训练前，使用随机的权重来判断图片，我们可以确定错误率接近100% 对模型进行训练 trained = NetTrain[net, trainingData, ValidationSet -> testData, MaxTrainingRounds -> 50 ] 从以上图表中我们大致可以看出正确率已经接近97% 再次预测上述图片，模型已经可以正确预测给出的图片数字为6 measurements = ClassifierMeasurements[trained, testData] 运行 measurements[“Accuracy”] 我们可以得到模型的正确率为98.02% ...