Blog share
DeepMind has published a paper that applies machine learning to pure mathematics to help mathematicians discover new theories in the field of pure mathematics.The paper focuses on the following two areas.

The most fundamental three-dimensional structure in Knot topology. Understanding the three-dimensional structural features of knot allows us to better bridge the gap between quantum field theory, non-Euclidean geometry, quantum mechanics, algebra, and geometry, and to study the relationships between the various branches of mathematics.
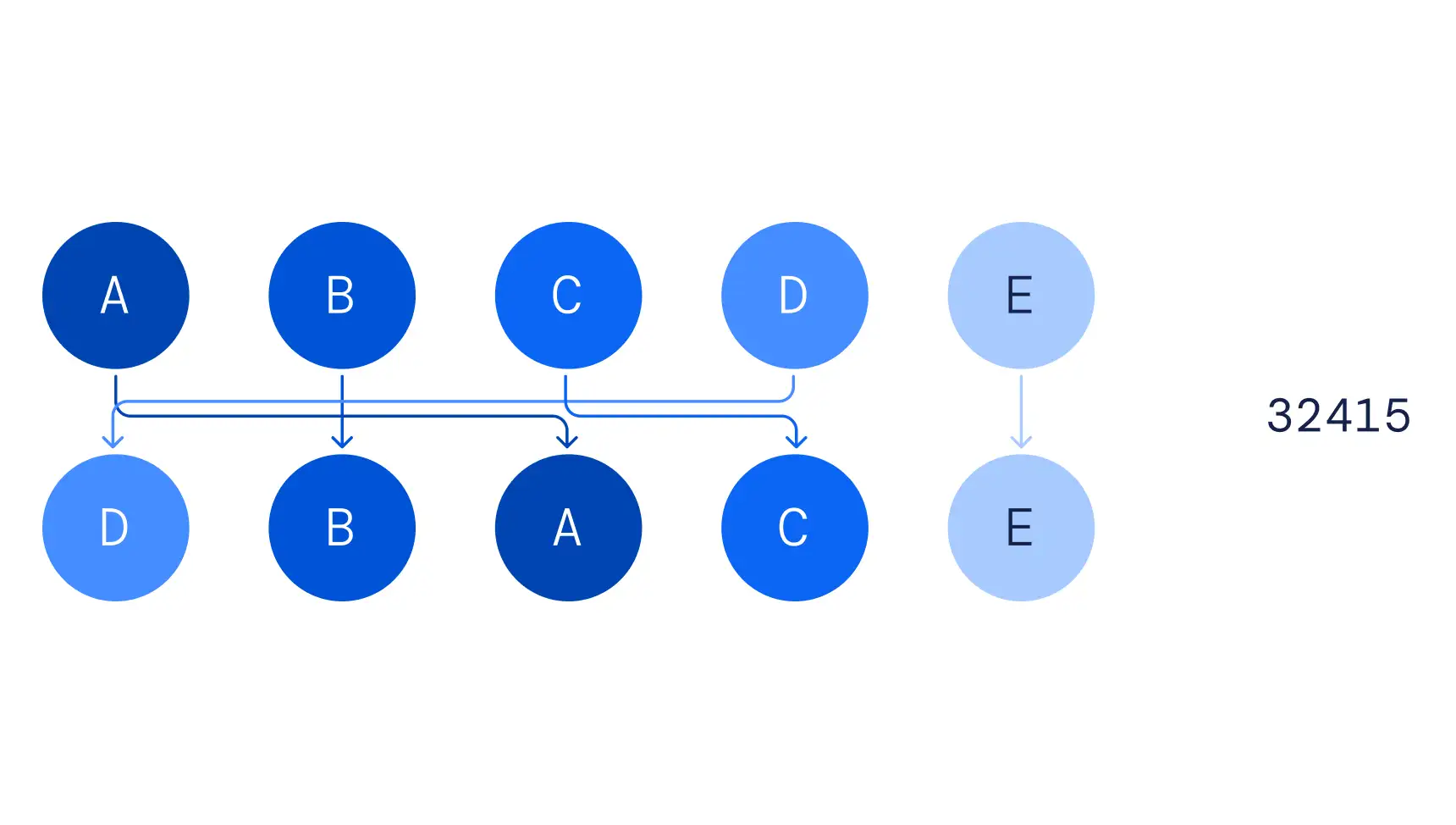
Arrange the combinations, 32415 represents moving the first element to the third position, the second element to the second position, the third element to the fourth position, and so on.
The article describes how ML aids mathematicians in the process of guessing to prove the theory from two mathematical fields.
Paper Interpretation
Machine learning methods combined with the study of pure mathematics can better discover new theories. We start with the simplest Euler formula, a polyhedron in 3D space, satisfying the following expression, Face + Vertices - Edges = 2, which semantically can be understood as, the number of faces + vertices - edges of a polyhedron = 2. Let X(z) ∈ Z2 × R2 and X(z) denote the number of vertices and edges of the polyhedron, and Y(z) ∈ Z is the number of faces of the polyhedron, then it can form an equation, X(z)(-1,1,0,0) = Y(z), f(X(z)) = X(z)(-1,1,0,0), this equation represents the relationship between the two-latitude polyhedron in three-dimensional space, the number of faces, the number of edges, and the number of vertices, when the latitude is extended to high latitude whether it still supports Similar expressions, the above expression conjecture in three latitude space we can guess the composition of the expression by traditional data-driven, in the case of high latitude, the problem will become very complicated. It is not possible to obtain reliable conclusions by traditional means.
The workflow in the above figure can be understood as follows.
-
the mathematician conjectures that there is some correspondence between X(z) and Y(z) f(x)=y
-
generate the data, select the data z of a particular distribution distribution state, get X(z), Y(z)
-
train the model based on the input X(z), output Y(z), and get the approximate guess function f
-
Understand the sensitivity of f to the variables in X(z) based on feature engineering
-
the mathematician further selects and optimizes the complete f function in his conjecture based on the f obtained by machine learning, thus completing the proof from conjecture to theory
This workflow guides the mathematician’s intuitive work in two ways:
-
machine learning is used to confirm the structural pattern relationships that already exist in mathematical conjectures.
-
by using feature techniques to help mathematicians understand these structural patterns.
The following describes the contribution of machine learning in pure mathematics through discoveries in two mathematical domains.
Topology
The study of topology at low latitudes is currently an active and mathematically influential field. knot are simple closed curves in three-dimensional space, and to classify these closed curves, we need knowledge from other fields to understand the properties in knot, where one of the properties is that any two knot, if they have algebraic or geometric invariants, then they both can be classified into the same class. Here we focus on two main ones, geometric invariants and algebraic invariants, which can be understood by referring to the following figure.
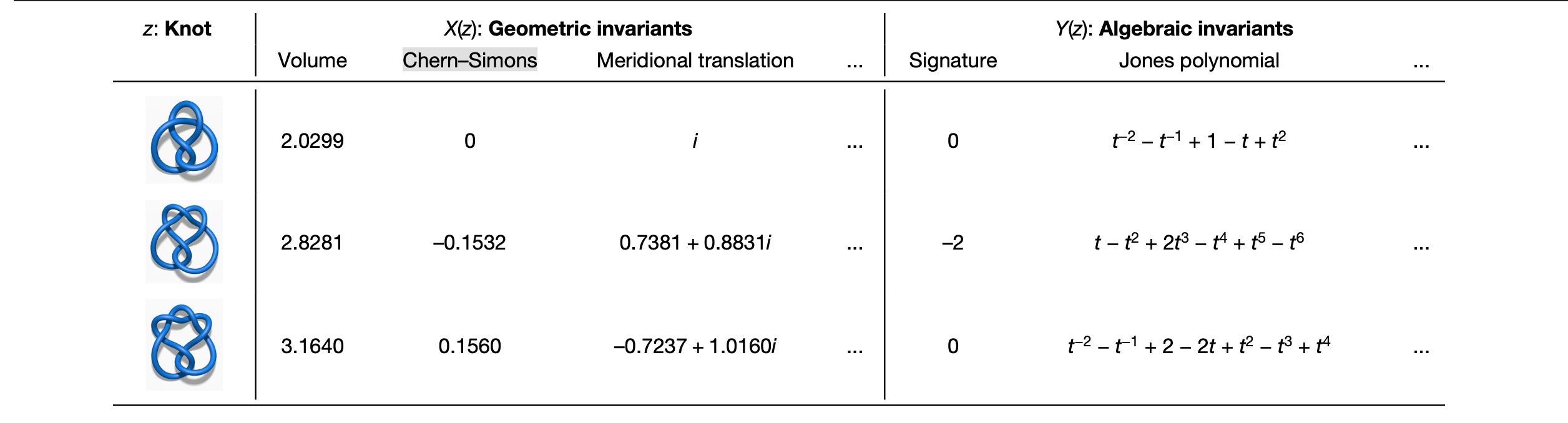
Through the machine learning model, we can find the relationship between the geometric and algebraic invariants, and then find which factors in X(z) Y(z) is more sensitive to through attribution analysis.
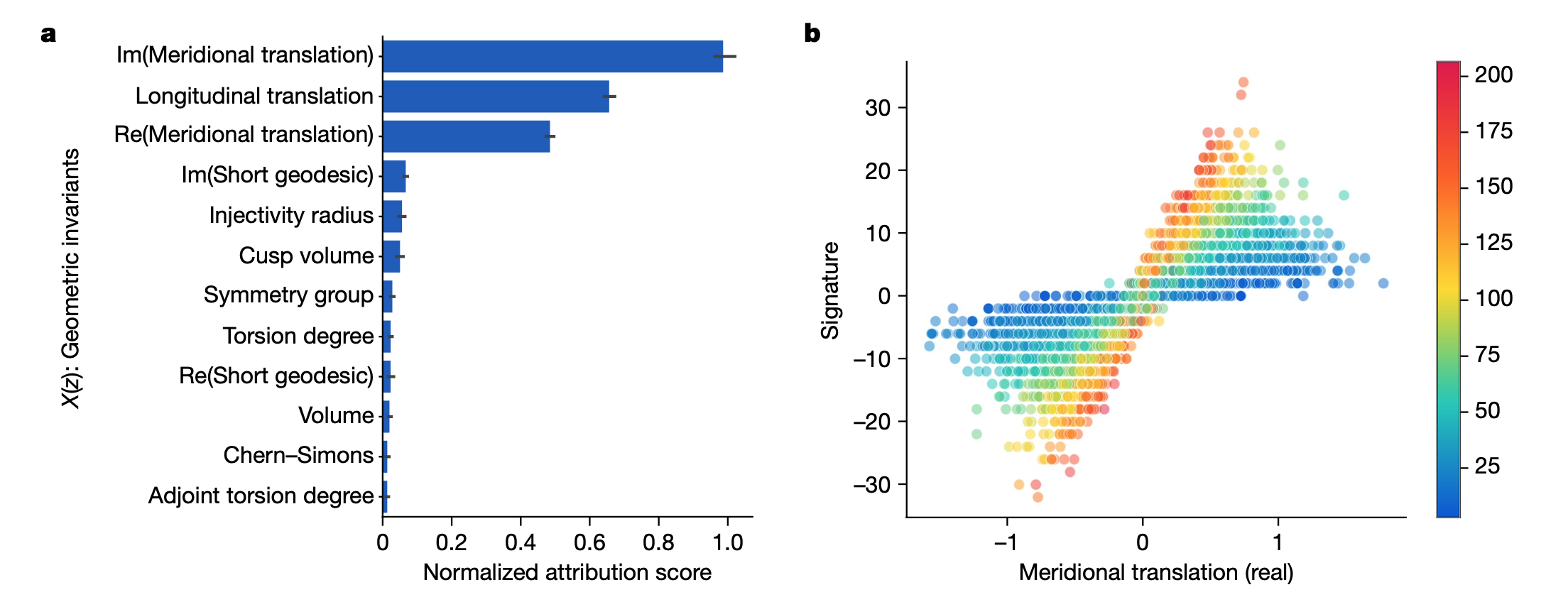
Finally, by introducing natural slope, slope(K) = Re(λ/μ), the meridional translation represents μ and the longitudinal translation represents λ.
Derive the theory: There exists a constant c such that for any hyperbolic knot K, there exists the inequality, |2σ(K)-slope(K)| ≤ cvol(K)inj(K)-3.
Denote the theory
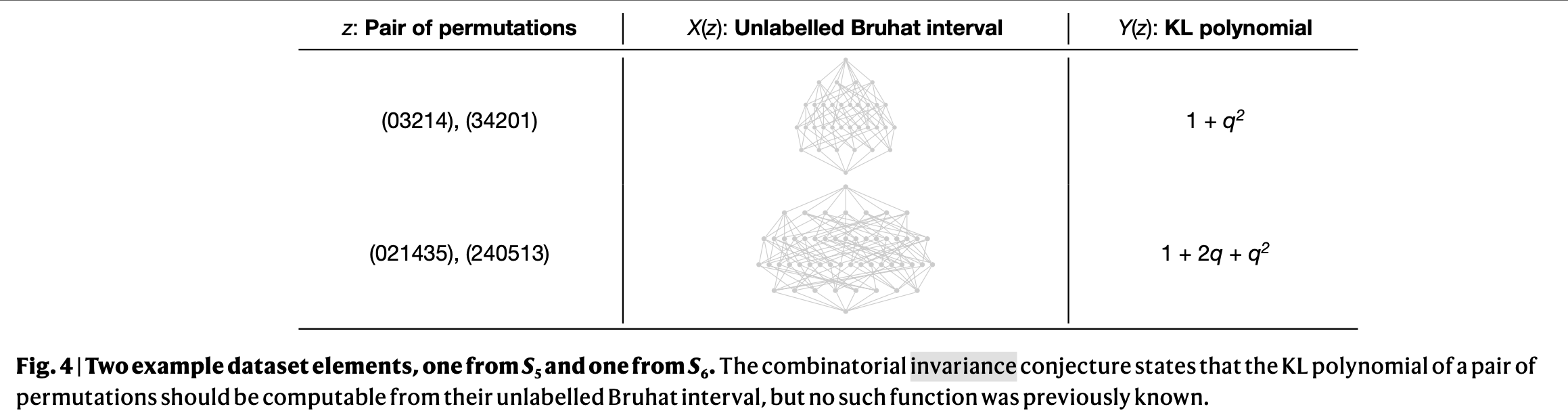
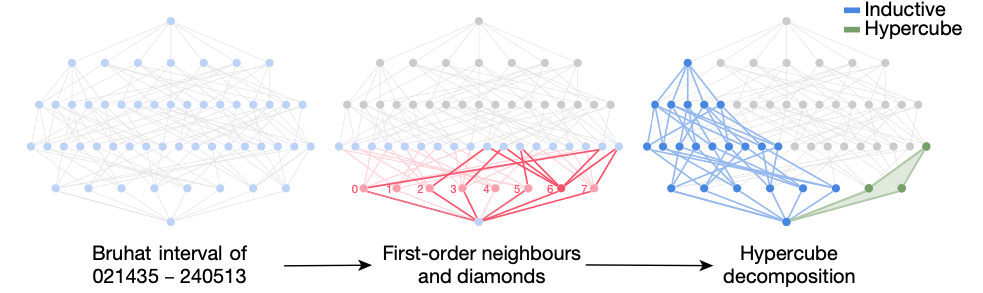
The combinatorial invariance conjecture states that the KL polynomial of a pair of permutations should be computable from its unlabeled Bruhat interval.
Through supervised learning, the model can compute KL polynomials from Bruhat intervals, and then through a series of inferences, mathematicians arrive at the following theory.
Each Bruhat interval has a typical hypercube decomposition along its polar reflection from which the KL polynomial can be computed directly.
Conclusion
Putting aside the above two areas of expertise in mathematics, applying machine learning to pure mathematics provides mathematicians with intuition and inspiration, opening a path for us to explore in machine intelligence. Although ML is only a layer of padding, this broadens the horizons of mathematicians. For the use of machine learning in the quantitative field, I also hold the same view, that is, ML is only an intermediate layer, he helps us to understand and statistical data, as for drawing a conclusion from a set of data, we need to rely on our own intuition to complete, ML can assist us to stimulate our intuition, so to do quantitative trading, what we need to learn behind the mathematical physics theory, in the data Backed by data, ML is used to verify our own theoretical conjectures, so that we can develop trading models that can win from the market.
References
Exploring the beauty of pure mathematics in novel ways
Towards combinatorial invariance for Kazhdan-Lusztig polynomials

