关于人工神经网络
人工神经网络模型判断手写数字
我们首先在Mathematica中徒手打造一个人工神经网络,然后对该神经网络进行训练,最后用训练得到的模型来判断图片上的手写数字是多少。
trainingData = ResourceData["MNIST", "TrainingData"];
testData = ResourceData["MNIST", "TestData"];
net = NetInitialize@NetChain[{
FlattenLayer[],
LinearLayer[500],
ElementwiseLayer["Sigmoid"],
LinearLayer[100],
ElementwiseLayer["Sigmoid"],
LinearLayer[10],
SoftmaxLayer[]},
"Input" ->
NetEncoder[{"Image", {12, 12}, "ColorSpace" -> "Grayscale"}],
"Output" -> NetDecoder[{"Class", Range[0, 9]}]]
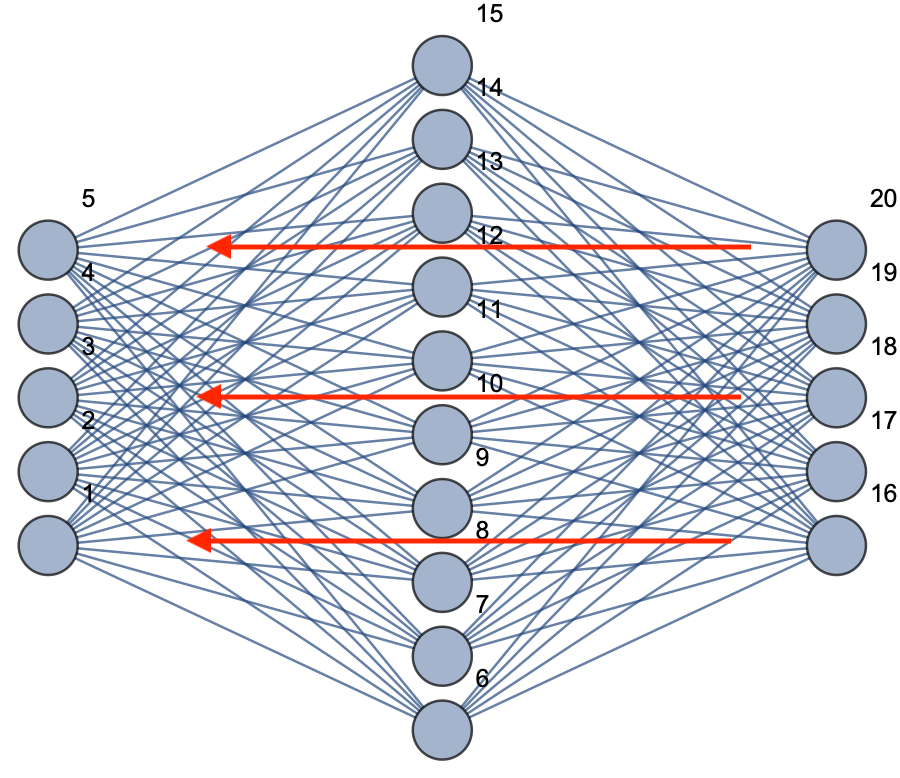
NetEncoder告诉我们输入的单通道12*12的图像 NetDecoder告诉我们我们的神经网络模型最后输出的是一个分类,类别分别是0-9中的一个数字 网络层的模型为:
- FlattenLayer[] 图像中的像素数据即两纬数据排列成一纬数据做为输入
- LinearLayer[500] 第一层线性层,输出数据为500个,限定函数为Sigmoid
- LinearLayer[100] 第二层线性层,输出数据为100个,限定函数为Sigmoid
- LinearLayer[10] 最后一层输出,因为我们需要有10个分类,所以这里设定是10,限定函数为 Softmax

神经网络层形象的展示如下:

训练数据标记,左边是实际的手写数字,右边是对应标签
RandomSample[trainingData, 10]

在未对模型进行训练前,使用随机的权重来判断图片,我们可以确定错误率接近100%

对模型进行训练
trained =
NetTrain[net, trainingData, ValidationSet -> testData,
MaxTrainingRounds -> 50 ]
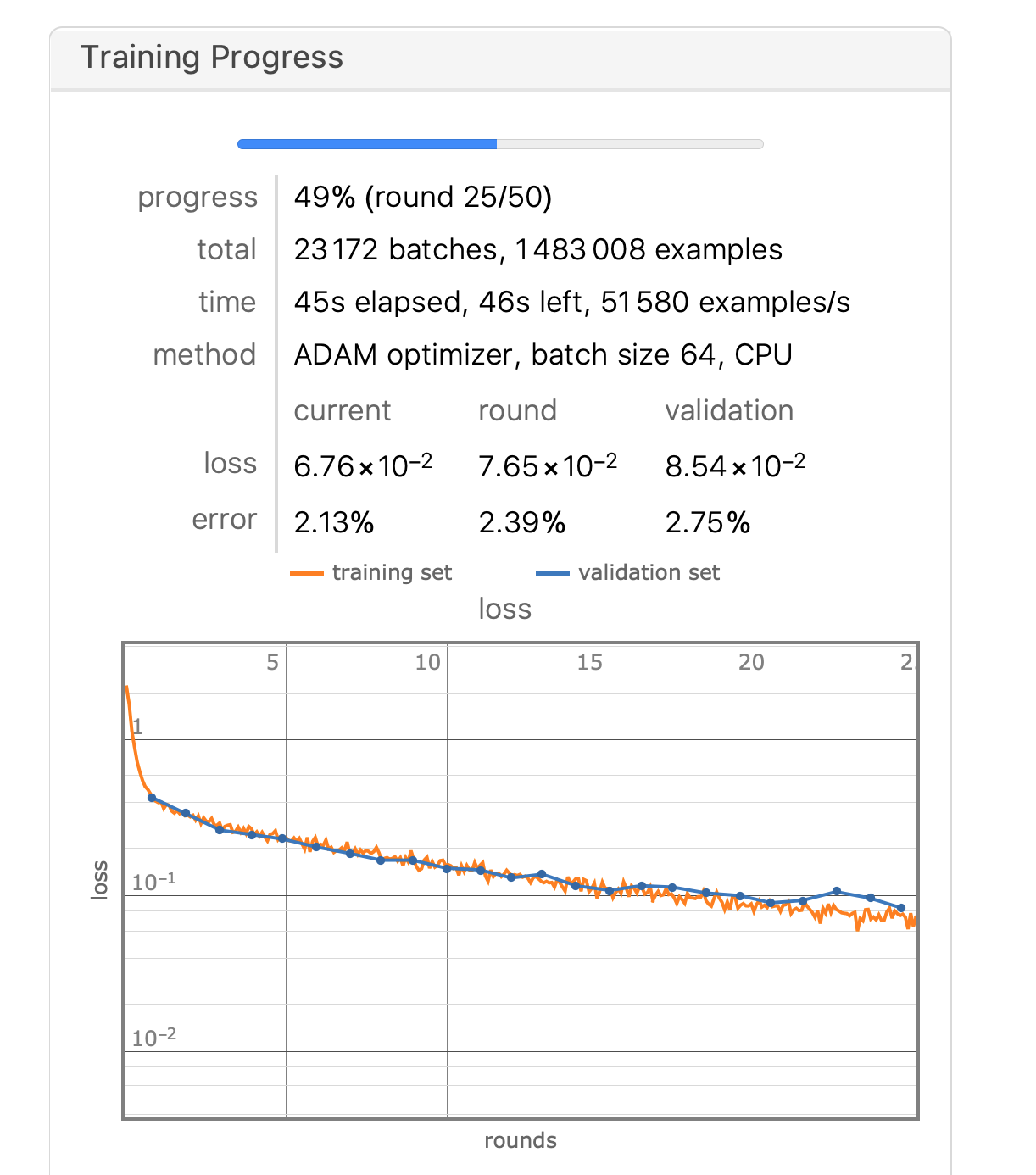
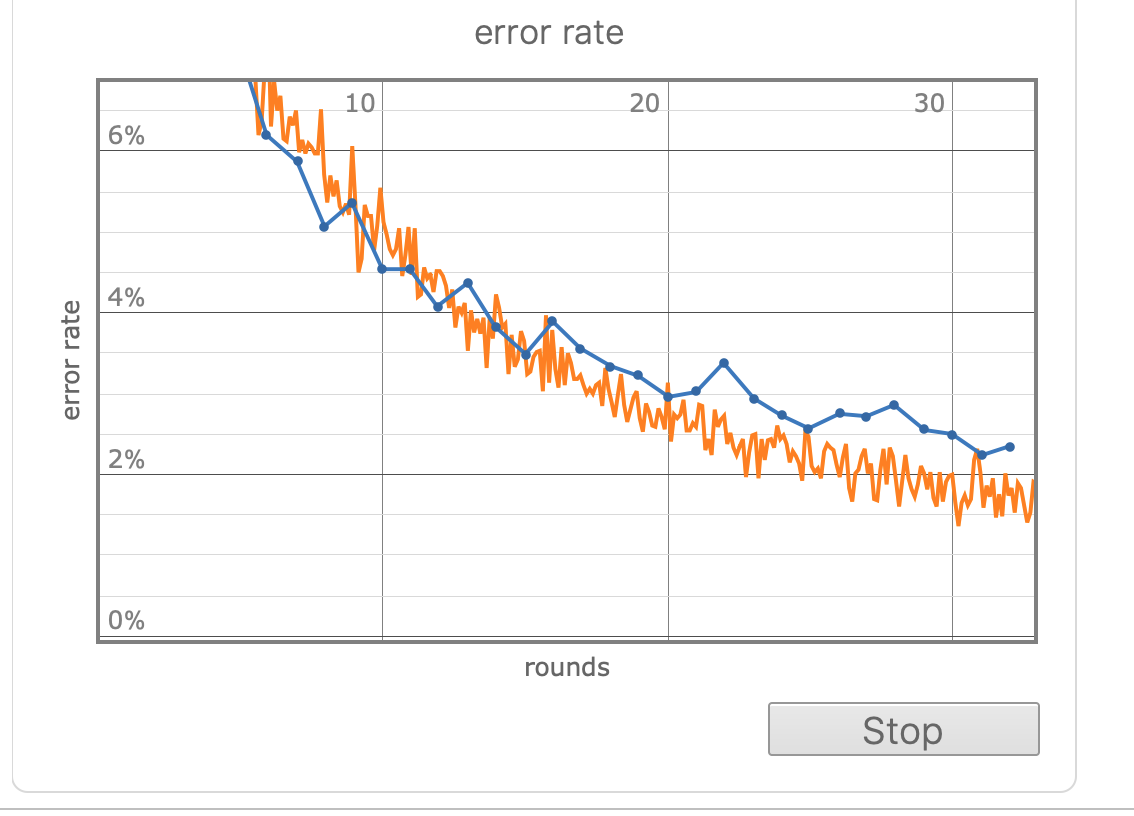
从以上图表中我们大致可以看出正确率已经接近97%
再次预测上述图片,模型已经可以正确预测给出的图片数字为6

measurements = ClassifierMeasurements[trained, testData]
运行 measurements[“Accuracy”] 我们可以得到模型的正确率为98.02%
模型中识别出错比较高的图片数字见下图:

训练得到的模型在推演中的混淆矩阵如下图所示:

神经网络中的反向传播推导
我们首先推导含有一个隐藏层的反向传播

对于反向传播中最重要的一个知识点就是链式求导法则,以下推理中我们首先假定不存在隐藏层和限定函数。





以上考虑的是神经网络没有隐藏层存在,且无限定函数,现在考虑网络中存在限定函数g,用来抑制神经元的输出。





从以上推论中我们可以知道反向传播中使用的方法就是链式求导法则,在反向传播中递归的修正每一层权重值,使得E接近局部极小值。
以上的推论和作图全部在Mathematica中完成,Notebook在这里下载。