卷积神经网络

关于卷积

可以抽象成数学表达式:

I可以表示一张图像的矩阵，K是卷积核

卷积的计算层

Object Recogition with Gradient-Based Learning

1. 输入层 Input Layer
2. 卷积层 Conv Layer
3. 限定层 RELU Layer
4. 池化层 Pooling Layer
5. 全连接层 Full connected Layer

创建网络 基础学习分辨猫狗归类

(* 创建模型 *)
myCatDogModel = NetChain[{
   ConvolutionLayer[32, 3], Ramp, PoolingLayer[2, 2],
   ConvolutionLayer[64, 3], Ramp, PoolingLayer[2, 2],
   FlattenLayer[],
   128,
   Ramp,
   2,
   SoftmaxLayer[]},
  "Input" -> NetEncoder[{"Image", {224, 224}, ColorSpace -> "RGB"}] ,
  "Output" -> NetDecoder[{"Class", {"cat", "dog"}}]]

(* 收集样本，训练集和测试集合 *)

(* 转换数据集合为Association格式 *)
dataSetsConvert[dateSets_] := Module[
  {},
  File[#] -> StringSplit[FileBaseName[#], "."][[1]] & /@ dateSets]
traingDataFiles = RandomSample[dataSetsConvert[traingData]];
testDataFiles = RandomSample[dataSetsConvert[testData]];

SetDirectory[
  "/Users/alexchen/datasets/Convolutional_Neural_Networks/dataset"];

FileNames["*.jpg", "training_set/cats/"];
FileNames["*.jpg", "training_set/dogs/"];
traingData = 
  Join[FileNames["*.jpg", "training_set/cats/"], 
   FileNames["*.jpg", "training_set/dogs/"]];
testData = 
  Join[FileNames["*.jpg", "test_set/cats"], 
   FileNames["*.jpg", "test_set/dogs"]];

(* 生成训练集和验证集 *)
traingDataFiles = RandomSample[dataSetsConvert[traingData]];
testDataFiles = RandomSample[dataSetsConvert[testData]];

(* 样本随机抽取显示 *)
RandomSample[traingDataFiles, 5]

(* 训练模型 *)
mytrainedModel = 
 NetTrain[catdogModel, traingDataFiles, All, 
  ValidationSet -> testDataFiles, MaxTrainingRounds -> 20] 

(* 生成训练模型评估报告 *)
myModelPlot = mytrainedModel["FinalPlots"]

(* 生成训练得到的模型计算模型正确率 *)
myTrainedNet = mytrainedModel["TrainedNet"]
ClassifierMeasurements[myTrainedNet, testDataFiles, "Accuracy"]

模型的损失和错误率

最终由 ClassifierMeasurements[myTrainedNet, testDataFiles, “Accuracy”] 得到的结果为 75% 即模型的准确率为75%

欠拟合及过拟合

从上述分析土里可以看出，橙色线(对训练集的学习)以及蓝色线(对验证集的推演)在最初的前五轮训练中是匹配下降的，在后面几轮训练中，模型出现对训练集合判断很准确，对验证集合的判断不再有任何改善反而出现了错误率上升的趋势，模型出现了过拟合.

当模型对验证集和训练集的拟合程度越好，则此模型的泛化能力越强.

关于卷积核KernelSize,Strid,PaddingSize

• KernelSize: 卷积核大小 比如 3 * 3

• Strid: 卷积核移动步长

• PaddingSize: 卷积核边界填充

• Dilation: 扩张卷积核

上述参数决定了我们卷积神经网络最后输出的结果维度

比如开头的模型，我们的输入图像为RGB三通道大小为{128,128}即张量形式为{3,128,128}，经过卷积核kernelSize{3,3}，Stride{1,1}，Paddingsize{{0,0},{0,0}}，Dilation{1,1}，之后我们得到的图像大小为{126,126}，图像经过卷积层过滤之后变小了，这是因为我们设定了PaddingSize边界填充为{{0,0},{0,0}}，{{0,0},{0,0}}可以理解为{{xBegin,xEnd},{yBegin,yEnd}}，这里x,y开始结束的偏移都为0，kernel在计算整个图像时，部分图像边界数据被丢失了，当我们添加PaddingSize->{{1,1},{1,1}}时经过卷积核处理之后图像的大小与原图像一致，都为{128,128}。

关于卷积层输出图像的维度计算

设输入的图像维度为graph = {g1,g2,g3,…,g(i)}，KernelSize = K，PaddingSize = {P_begin, P_end}，Strid = S，Dilation = Df，计算输出图像的维度为d = {d1,d2,d3,…,d(i)}:

d(i) = (g(i) + P_begin + P_end - ((Df - 1) * (K - 1) + K))/S + 1 结果取整

化简等式为:

d(i) = (g(i) + P_begin + P_end - Df(K - 1) - 1)/S + 1 结果取整

根据 PaddingSize 为 {0,0} 和 {1,1}，我们可以计算得到输出的维度分别为{126,126}和{128,128}。

如果 ConvolutionLayer[64, 3, PaddingSize -> 1, “Stride” -> 2] 即移动步长为2，那么根据上述公式我们得到最终的维度输出维度为{64,64}，图像被裁剪成原来的一半。ConvolutionLayer[64, 3, PaddingSize -> 1, “Stride” -> 3]，图像被裁剪到{43,43}。

同样采用扩张参数 ConvolutionLayer[64, 3, PaddingSize -> 1, Dilation -> 2]，我们得到的输出图像被裁减到{126,126}，ConvolutionLayer[64, 3, PaddingSize -> 1, Dilation -> 3]，图像被裁剪到{124,124}。

关于池化层的维度计算

池化层的作用是降低图像的维度，但保留重要信息。

MaxPoolinglayer参数分别为:

• Kernelsize: 计算核大小

• Stride: 移动步长

• Paddingsize: 边界填充大小

池化层的维度输出计算方式可以类比卷积层的输出维度计算方式，

池化层的Df=1

d(i) = (g(i) + P_begin + P_end - K)/S + 1 结果取整

比如 Paddingsize = {0,0}，kernelsize = {2,2}，Stride S = {2,2}，那么计算输出维度为 (128 + 0 + 0 - 2)/2 + 1 = 64，如果kernelsize = Stride = {3,3}，那么计算输出维度为{42,42}。

迁移学习

迁移学习就是在已经训练好的模型上，冻结特性层，只学习最后几层的权重值，进而获得满足自己需求的神经网络。

采用 VGG6 深度学习模型

VGG-16 Trained on ImageNet Competition Data

vgg16Model = NetModel["VGG-16 Trained on ImageNet Competition Data"]

VGG16中包含了大量的卷积层，为了对图片中的特征进行过滤和匹配

VGG16可以辨别1000中图像中的物体，目前我们只需要辨别狗🐶和猫🐱就可以了，所以需要修改神经网络的最后几层。

获得到倒数第四层的整个网络

tempNet = 
 Take[NetModel[
   "VGG-16 Trained on ImageNet Competition Data"], {1, -4}]
   
newNet = NetChain[<|"pretrainedNet" -> tempNet, 
   "linearNew" -> LinearLayer[], "softmax" -> SoftmaxLayer[]|>, 
  "Output" -> NetDecoder[{"Class", {"cat", "dog"}}]]

训练模型，并且冻结除**linearNew**层之外的其他层的权重

trainedNet = NetTrain[newNet, RandomSample[traingDataFiles, 1000], 
  ValidationSet -> RandomSample[testDataFiles, 10], 
  MaxTrainingRounds -> 3, 
  LearningRateMultipliers -> {"linearNew" -> 1, _ -> 0}]

最后验证迁移学习的正确率，随机从验证集合中抽取5张图片正确率为100%

从网络上随机挑选一张的猫图片，验证模型的预测是否正确:

卷积层的中间过程

首先获得第一个卷积层conv1_1的特征输出(总共64个特征输出):

convFeatures = trainedNet[🐱的图像,NetPort[{"pretrainedNet/conv1_1", "Output"}]];
Dimensions[convFeatures] (* output:  {64, 224, 224} *)
ImageCollage[Map[ImageAdjust@*Image, convFeatures], 
 ImageSize -> Medium]

同样的方式我们可以获得第一个池化层的输出图像:

convFeatures = trainedNet[🐱的图像,NetPort[{"pretrainedNet/pool1", "Output"}]];
Dimensions[convFeatures] (* output: {64, 112, 112} *)
ImageCollage[Map[ImageAdjust@*Image, convFeatures], 
 ImageSize -> Medium]

可以看出，池化层将图像数据集减少一半，但是保留其中的重要信息，这样有利于降低训练过程中对计算资源的消耗。

获得pretrainedNet/conv2_1特征的输出(总共128个特征):

convFeatures = trainedNet[🐱的图像,NetPort[{"pretrainedNet/conv2_1", "Output"}]];
Dimensions[convFeatures] (* output: {128, 112, 112} *)
ImageCollage[Map[ImageAdjust@*Image, convFeatures], 
 ImageSize -> Medium]

池化层的输出:

以此类推，我们得到第三个大层的pretrainedNet-conv3_1特征的输出(总共256个特征)

池化层的输出:

我们可以看出卷积神经网络在不断的缩小特征范围，从最开始的获取猫的整个轮廓特征到获取猫的耳朵眼睛鼻子等边缘轮廓，再细分到对眼睛耳朵的具体特征描述比如大小，和其他特征之间的距离位置信息，寻找鼻子耳朵腿等边缘细节特征。

第四个大层的pretrainedNet/conv4_1特征输出(总共512个特征)

从中我们可以发现神经网络通过卷积核来扫描整个图像，初始层检测图像中物体的边缘轮廓，然后越高的层越细化图像中的特征，比如寻找猫的耳朵，猫的眼睛，猫的嘴巴，猫的毛发。

每一层的卷积核都代表着一种特征表述:

weights = 
  NetExtract[trainedNet, {"pretrainedNet/conv1_1", "Weights"}];
ImageAdjust[Image[#, Interleaving -> False]] & /@ Normal[weights]

第一层的卷积核可视化表述如下(总共64个卷积核):

第二层卷积核可视化表述:

算法

卷积神经网络前向计算类似人工神经网络，以下两表达式分别表示通道数为1和通道数为C的卷积网络前向计算表达式。

I 表示图像矩阵，K表示卷积核，为了方便与传统矩阵对应，m,n从1开始迭代，C代表图像的通道，灰度图的通道数为1，带颜色的图像通道数为3即RGB三通道，b代表偏置。

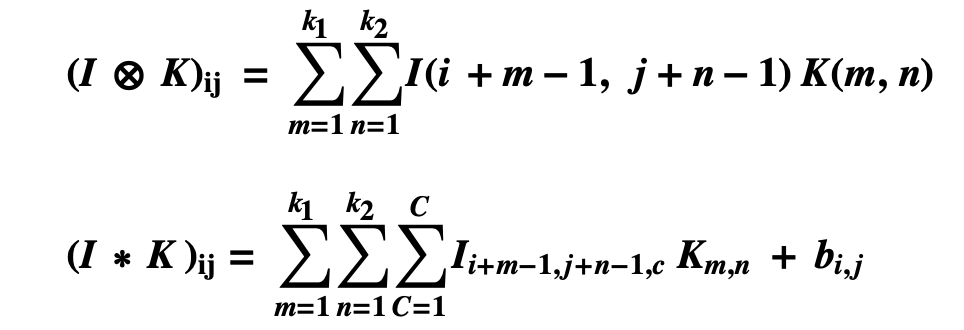
卷积神经网络的反向传播

卷积网络反向传播的计算方式也类似与人工神经网络的反向传播计算方式，因为推导反向传播比较复杂，并且很有可能在推导过程中使用了错误的计算方式，所以这一块的算法推导，我会独立放到DeepMind UCL课程第二课人工神经网络与第三课卷积神经网络的总结中去严密的推导这两种类型网络的反向传播。