Lotka Volterra 方程
维基百科解释: Lotka Volterra
该方程组描述了 捕食系统模型 微分方程为:
dx/dt = Axy - Bx
dy/dt = Cy - Dxy
=>
dy/dx = (Cy - Dxy) / (Axy - Bx) (1.1)
{A, B, C, D} 均为模型系数
对微分方程(1.1)求解为:
 W 为Lambert W function
W 为Lambert W function
当系数为 {A -> 0.1, B -> 2, C -> 4, D -> 0.4, x -> {1,30}} y[x]

由于我们需要获得 x,y 关于自变量时间t,在模型系数{A,B,C,D}下的模型图,所以在Mathematica中对该方程组定义和设置模型系数
 求该方程的数值解
求该方程的数值解
 创建Modelica模型 在0时刻 x[0] = 10, y[0] = 5
创建Modelica模型 在0时刻 x[0] = 10, y[0] = 5
model = CreateSystemMod["Hare",
Join[predatorPreyEq, {x[0] == 10, y[0] == 5}], t,
Association[{"ParameterValues" -> params}]]
建模
Modelica 模型源码
model Hare
parameter Real alpha = 0.1;
parameter Real beta = 2;
parameter Real gamma = 4;
parameter Real sigma = 0.4;
Real x;
Real y;
initial equation
x = 10;
y = 5;
equation
der(x) = (-1) * beta * x + alpha * x * y;
der(y) = gamma * y + (-1) * sigma * x * y;
»;
end Hare;
在SystemModeler中建模得到的x,y随着时间变化的关系图

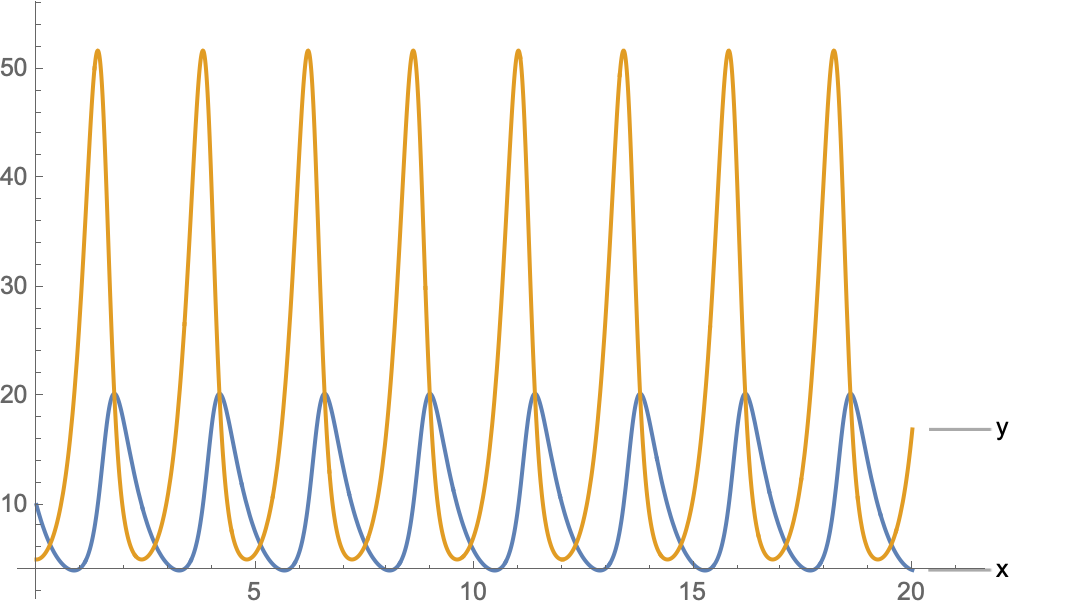
特别的当 alpha = beta = gamma = sigma = 1时


扩展练习
Doing