SIR Modeling
SIR 经典模型主要是在传染病领域用来预测感染人数的未来趋势。
S[t] 表示susceptible易感人群
I[t] 表示infected已经感染的人群
R[t] 表示recovered已经康复人群
参考:
MathWorld:
Kermack-McKendrick Model
Kermack-McKendrick 最初的模型是为了解释像在1665-1666年发生的鼠疫,1865年发生的霍乱,感染人群的数量随着时间的变化。 该模型假定总人口是是固定的,传染病的潜伏期是瞬间的,传染持续时间与疾病的周期相同,并且假定人群都是无差异的,无性别及种族差异。
该模型使用了三个非线性常微分方程:
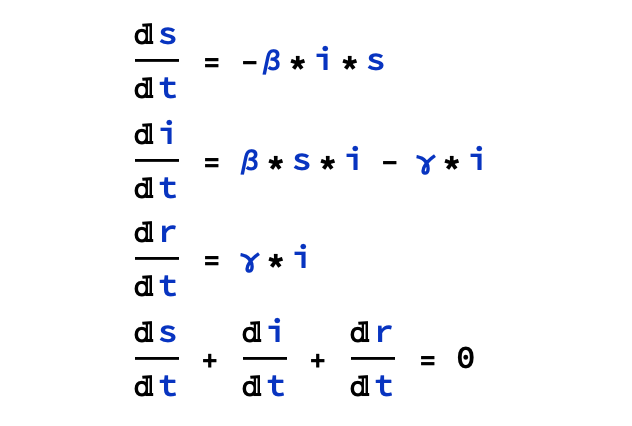

- beta 表示 infection rate 感染率
- gamma 表示 recovery rate 恢复率
- i 表示已感染人群
- r 表示已恢复健康的人群
- s 表示易感染人群
预设值: beta = 20%, gamma = 15%, i(0) = 0.1, r(0) = 0, s[0] = 10
Modelica 源码
model SIRModel
parameter Real beta = 0.2;
parameter Real gamma = 0.15;
Real i;
Real r;
Real s;
initial equation
s = 10;
i = 0.1;
r = 0;
equation
der(s) = (-1) * beta * i * s;
der(i) = (-1) * gamma * i + beta * i * s;
der(r) = gamma * i;
end SIRModel;
模型预测图:
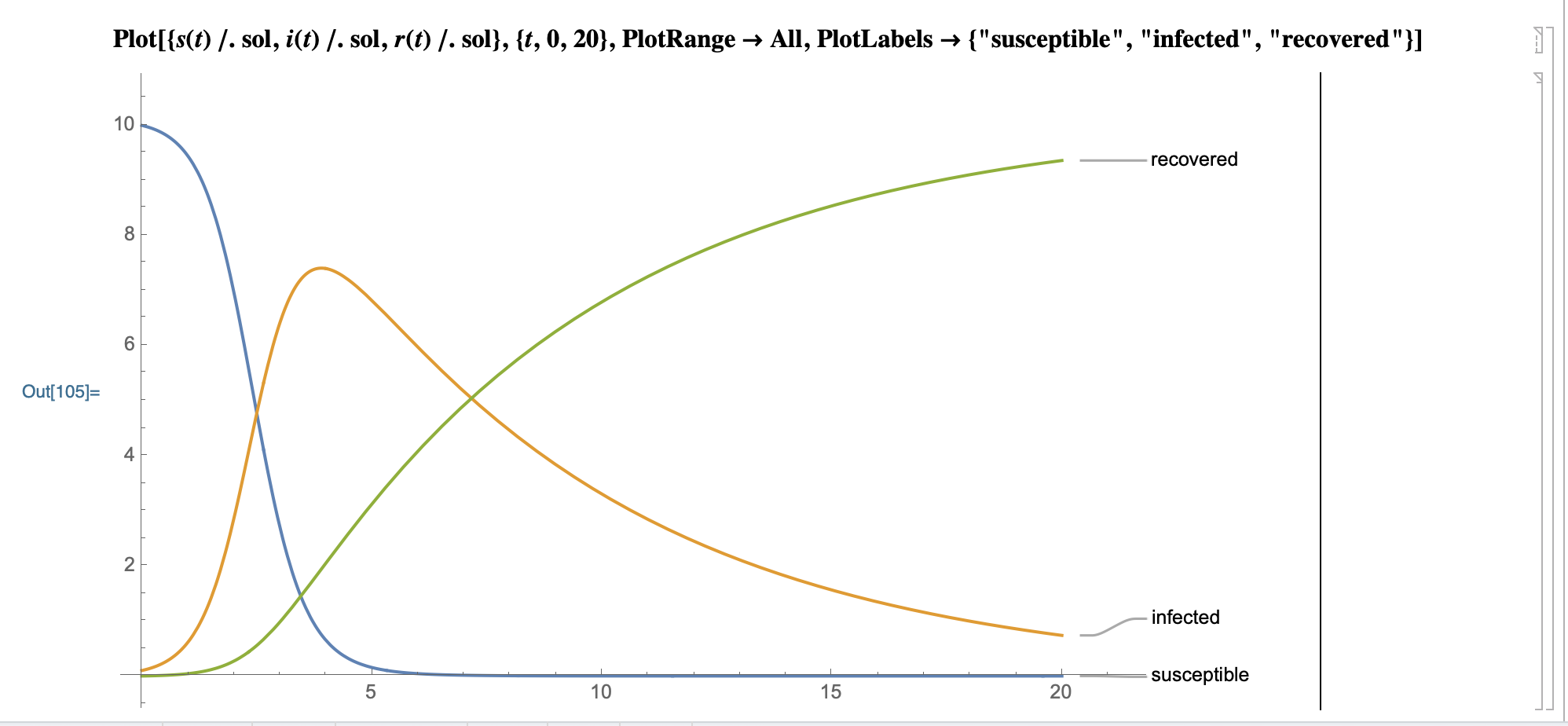
SystemModeler 预测图

SEIR Model
Doing