DeepMind UCL 深度学习在线课程2总结

神经网络基础

June 9, 2020

2 分钟

历史

最初的神经网络开发思路来自于人类对大脑的研究，大脑中存在着大量的生物神经元，如上图所示。生物神经元模型中电信号通过树突(Dendrite)流入细胞体(Cell body)，细胞体相当于一个数据处理中心，当存在足够的刺激反应后，它发送一个微弱的电信号到类似电缆线状的轴突(Axon)上，电信号流经轴突然后到达神经断端(Synaptic terminals)，一个神经元会有多个树突和单独一个轴突，神经元和神经元之间的信号传递通过突触间隙的导电流体完成，通过对生物神经元建模，就得到了人工神经元，建立对应模型的四个要素如下：

生物模型:

细胞体
轴突
树突
突触

人工神经元:

细胞体
输出通道
输入通道
权重

McCulloch和Pitts根据生物神经网络开发出了第一个人工神经元模型。论文地址 A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY

神经元模型:

机器学习

深度学习只是机器学习集合里面的一个子集，以下对机器学习总的概括。

监督学习

算法:

k-Nearest-Neighbors
Linear Regression
Logistic Regression
Support Vector Machine
Decision Trees
Random Forests
Neural networks

无监督学习

算法:

Clustering
- K-Means
- DBSCAN
- HCA (Hierarchical Cluster Analysis)
Anomaly detection and novelty detection
- One Class SVM
- Isolation Forests
Visualization Dimensionality reduction
- PCA (principal component analysis)
- Kernel PCA
- Locally Linear Embedding (LLE)
- t-distributed stochastic neighbor embedding (t-SNE)
Association rule learning
- Apriori
- Eclat

神经网络架构

神经网络可以类比成对图的计算，简单梳理了较常用的神经网络架构:

DNN (deep neural networks)

CNN (Convolutional neural network)

RNN (Recurrent neural network)

AutoEncoders

Deep Belief Networks DBNs
Restricted Boltzmann Machines (RBMs)
Emergent Architectures (EAs)
- Deep Spatio Temporal Neural Network
- Mutli-Dimensional Recurrent Neural Network
- Convolutional AutoEncoders

人工神经网络算法

人工神经网络的计算方式如上y为输出神经元，x为输入神经元，b为偏置，w为神经元之间的连接权重。

上述我们定义了一个输出大小为10的向量，输入向量大小为5，权重为10*5矩阵，权重层大小为10的单层神经网络。

在上图计算中，我们输入向量{1,2,3,4,5}到神经网络中得到输出为{-0.808207, -1.06912, -2.05227, 3.40917, 2.20901, -3.62218, 5.72408, -0.997228, 2.31316, 1.08206}

从神经网络中我们获得权重和偏置的值，我们可以验证人工神经网络的计算方式wx + b = y，linearLayerWeights 点乘 input + linearLayerBias 所获得的输出值与上图一致。

梯度下降算法

关于梯度的计算:

R->R
R^(n) -> R^(n)

向量场 Vector Field:

设z = f(x,y) = x^2 + y^2

Mathematica代码如下:

f[x_, y_] = x^2 + y^2;
Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3}, PlotStyle -> Gray]

计算f(x,y)梯度:

grad = Grad[f[x, y], {x, y}] (* output: {2x, 2y}
VectorDensityPlot[grad, {x, -3, 3}, {y, -3, 3}, 
 PlotLegends -> Automatic, ColorFunction -> "Rainbow"]

梯度的向量场可以理解成

我们所定义函数的梯度向量场如下所示，颜色代表向量的长度:

从图中我们可以看出随着x,y的变化，函数f(x,y)在各点的梯度变化情况。

根据梯度寻找最小值:

(* 计算梯度 *)
grad = Grad[f[x, y], {x, y}]
(* {2 x, 2 y} *)

(* 解梯度方程，当梯度为0时，函数存在极大或者极小值 *)
sol = NSolve[grad == {0, 0}, {x, y}, Reals]
(* {{x -> 0, y -> 0}} *)

(* 再求梯度的一阶导数,大于0时，函数存在极小值，小于0时，函数存在极大值 *)
dGrad = Grad[grad, {x, y}]
(* {{2, 0}, {0, 2}} *)

Show[
 Plot3D[f[x, y], {x, -3, 3}, {y, -3, 3},
  PlotStyle -> Opacity[.4]],
 Graphics3D[{PointSize[.04], Red, Point[{x, y, f[x, y]}] /. sol}]]

得到函数的极小点{x->0,y->0,z->0}

计算函数的梯度以及梯度的一阶导数，就可以帮助我们判断函数的极值点。在神经网络中依靠梯度下降算法，不断的迭代改变权重的值，从而使得损失函数达到极小值。

利用泰勒展开式，我们可以证明当变量x按照梯度递减的计算方式，使得f(x)逐渐逼近极值。

为什么要使用激活函数

为什么要使用激活函数，首先看下XOR异或运算

{1,1} -> 0
{0,0} -> 0
{1,0} -> 1
{0,1} -> 1

我们需要训练一个模型使得该模型能够预测XOR的计算。

第一模型: 无隐藏层的单一模型:

data = {{1, 1} -> 0, {0, 0} -> 0, {1, 0} -> 1, {0, 1} -> 1}
net = NetChain[{LinearLayer[1]}]
trained = NetTrain[net, data]
trained[#] & /@  Keys[data]

(* Output: {0.5, 0.5, 0.5, 0.5} *)

我们可以看到该模型无法预测简单的XOR规则。

第二个模型增加隐藏层

net = NetChain[{LinearLayer[16], 1}]

(* Output {0.500014, 0.500002, 0.500009, 0.500006} *)

我们还是发现更改后的模型无法预测XOR。

第三个继续增加模型的隐藏层的层数

net = NetChain[{LinearLayer[16], LinearLayer[16], 1}]

output -> {0.499969, 0.499997, 0.499982, 0.499984}

显然该模型也无法满足要求。由于模型采用的算法是y=wx+b的线性回归算法，无法表示XOR运算，所以需要在网络中加入非线性的特性，比如在隐藏中加入ReLU激活函数(整流线性单元)

net = NetChain[{LinearLayer[16], Ramp, 1}]

output -> {4.38886*10^-8, 2.32831*10^-10, 1., 1.}

加入非线性的特性的之后，我们的网络就能正确表达XOR运算。

反向传播数学推论

先介绍微积分中的链式求导法则如下图:

向量记法:

激活函数

Sigmoid
Relu
Tanh
softmax
Cross entropy

关于反向传播的推导

神经网络在计算过程中其实就是对图的计算，首先考虑不含隐藏层的人工神经网络:

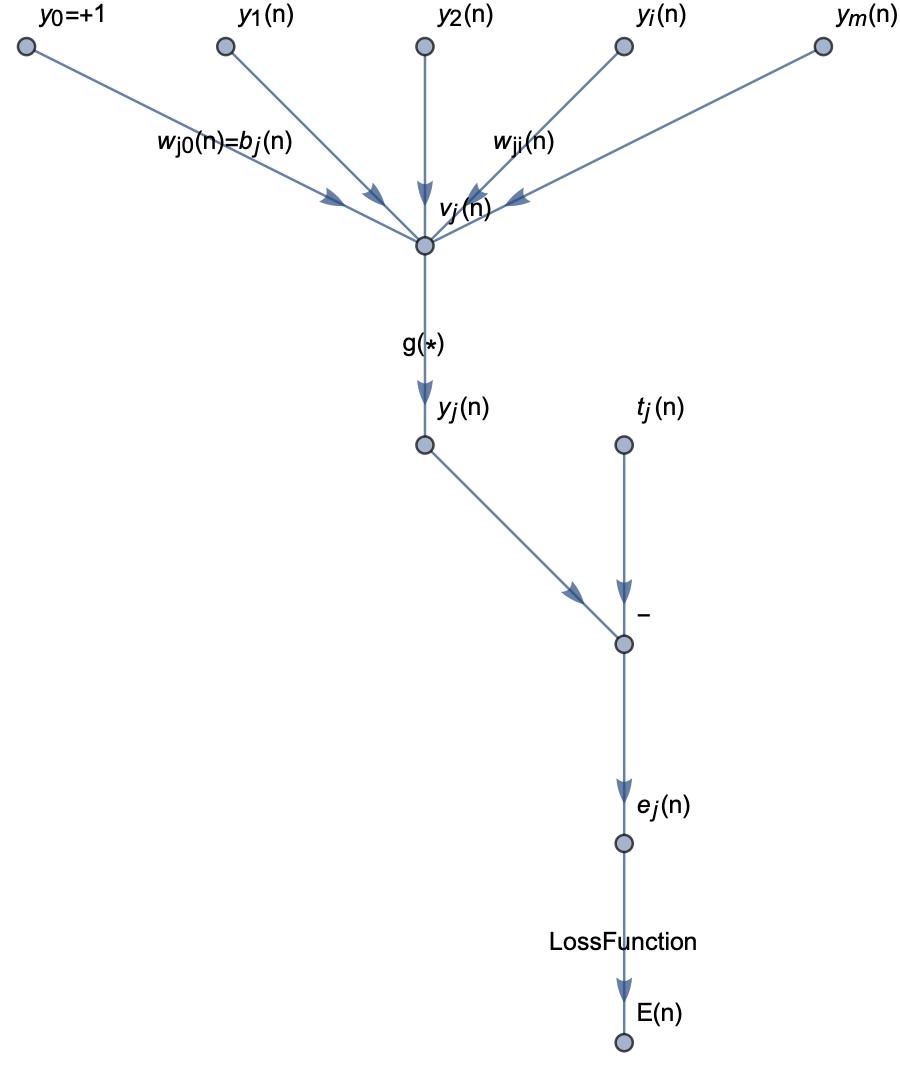
g代表限定函数，E代表所有输出层的误差和，yj表示计算值，tj代表目标值，根据监督学习的理论，我们需要计算计算值与目标值的差距，使得这个差距越小越好，网络中我们能够调整的参数就只有权重和阀值，为了使得误差最小，我们必须细微的调整权重，使得误差越来越小，其中的计算方式就是采用梯度下降算法，修改网络层中的权重值就是神经网络的反向传播算法。

反向传播推导过程如下: