Pure Mathematics With Machine Learning

December 6, 2021

alexchen

1 分钟

博客分享

DeepMind 发表了一篇论文，将机器学习应用于纯数学领域，帮助数学家在纯数学领域中发现新的理论，论文主要从以下两个领域入手。

Knot拓扑学中最基本的三维结构，了解knot的三维结构特征，让我们能够更好的在量子场论，非欧几里得几何学，量子力学，代数学，几何学之间架起桥梁，研究数学各个分支之间的关系。

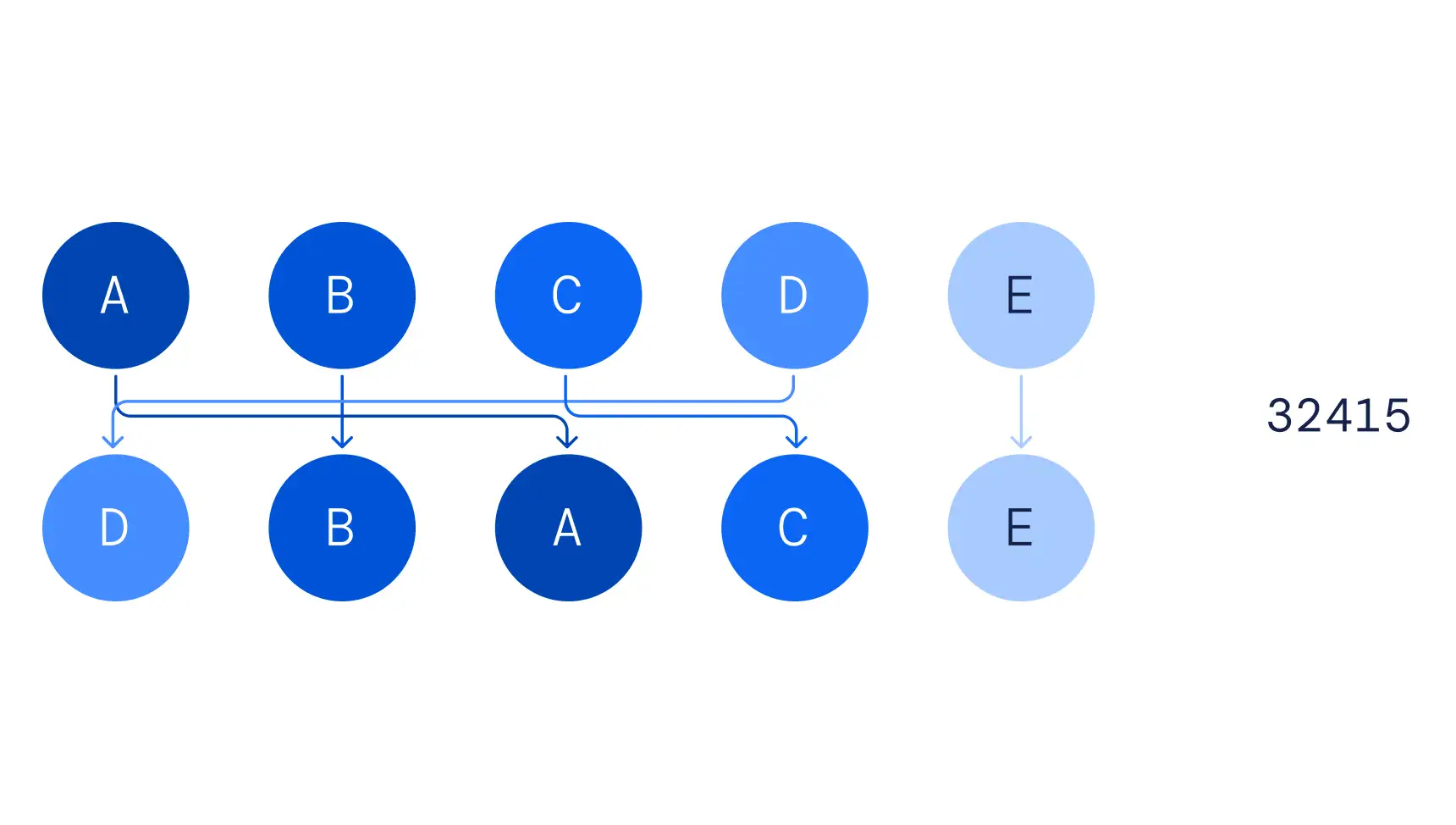
排列组合，32415 代表着将第一个元素移动到第三个位置，第二个元素移动到第二个位置，第三个元素移动到第四个位置，以此类推。

文章从两个数学领域介绍了ML是如何辅助数学家完成理论的猜测到证明这一过程。

论文解读

机器学习方法与研究纯数学的方法相结合能够更好的发现新理论，我们从最简单的欧拉公式开始，在三维空间中的一个多面体，满足如下表达式，Face + Vertices - Edges = 2，语意上可以理解为，多面体的面数 + 顶点数 - 边数 = 2，设X(z) ∈ Z2 × R2，X(z)表示多面体的顶点数和边数，Y(z) ∈ Z 是多面体的面数，那么就可以构成一个方程，X(z)(-1,1,0,0) = Y(z)，f(X(z)) = X(z)(-1,1,0,0)，这个方程代表着三维空间中两纬多面体，面数，边数，顶点数之间的关系，当纬度扩展到高纬时是否还支持类似的表达式，三纬空间的上述表达式猜想我们可以通过传统的数据驱动去猜测表达式的构成，在高纬的情况下，问题将变得非常复杂。无法通过传统的方式去获得可靠的结论。

上图中的工作流可以理解为：

数学家猜想X(z)和Y(z)之间存在某种对应关系f(x)=y
生成数据，选取特定分布分布状态的数据z，得到X(z)，Y(z)
根据输入X(z)，输出Y(z)，训练模型，得到近似的猜想函数f
根据特征工程理解f对于X(z)变量中的敏感度
数学家根据机器学习得到的f，进一步选择和优化自己猜想中的完整f函数，从而完成从猜想到理论的证明

该工作流从两方面来指导数学家的直觉工作:

通过机器学习来确认数学猜想中已经存在的结构模式关系。
通过特征技术帮助数学家理解这些结构模式。

以下通过两个数学领域的发现来描述机器学习在纯数学领域的贡献。

拓扑学

目前低纬度的拓扑学研究是一个活跃的在数学上具有影响力的领域，knot是三维空间中简单的闭合曲线，对这些闭合曲线进行分类，我们需要通过其他领域的知识来了解knot中的属性，其中一个属性是任意两个knot，如果他们存在代数或者几何上的不变量，那么他们两者就可以归为同一个类。在这里我们主要关注两个，几何不变量和代数不变量，可以参看下图了解这两大不变量。

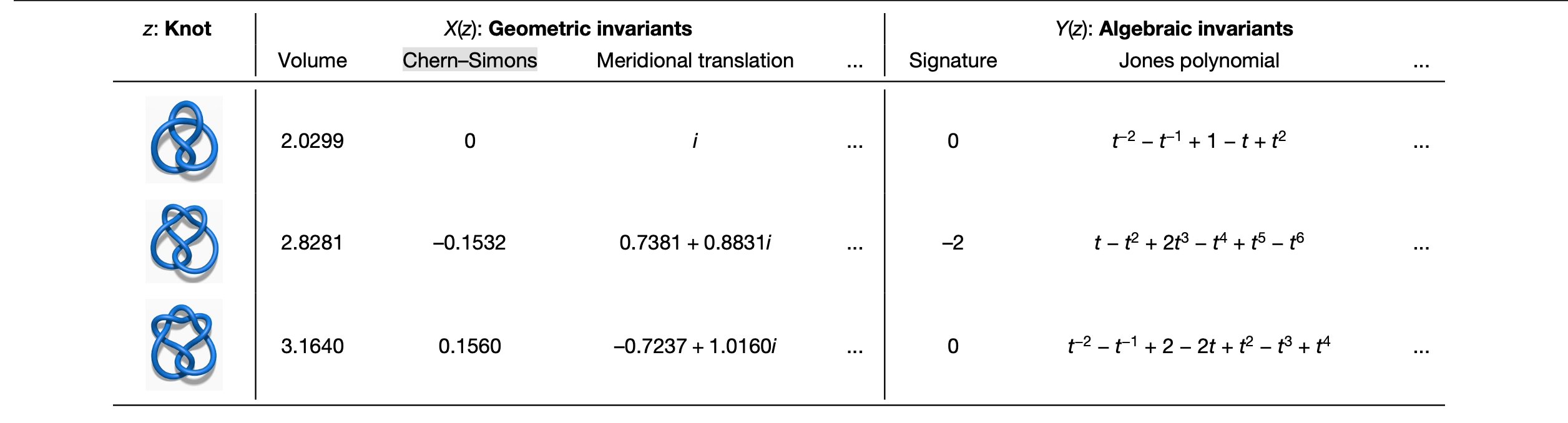
通过机器学习模型，我们可以发现几何不变量与代数不变量之间的关系，再通过归因分析，找到Y(z)对于X(z)中的哪些因子比较敏感。

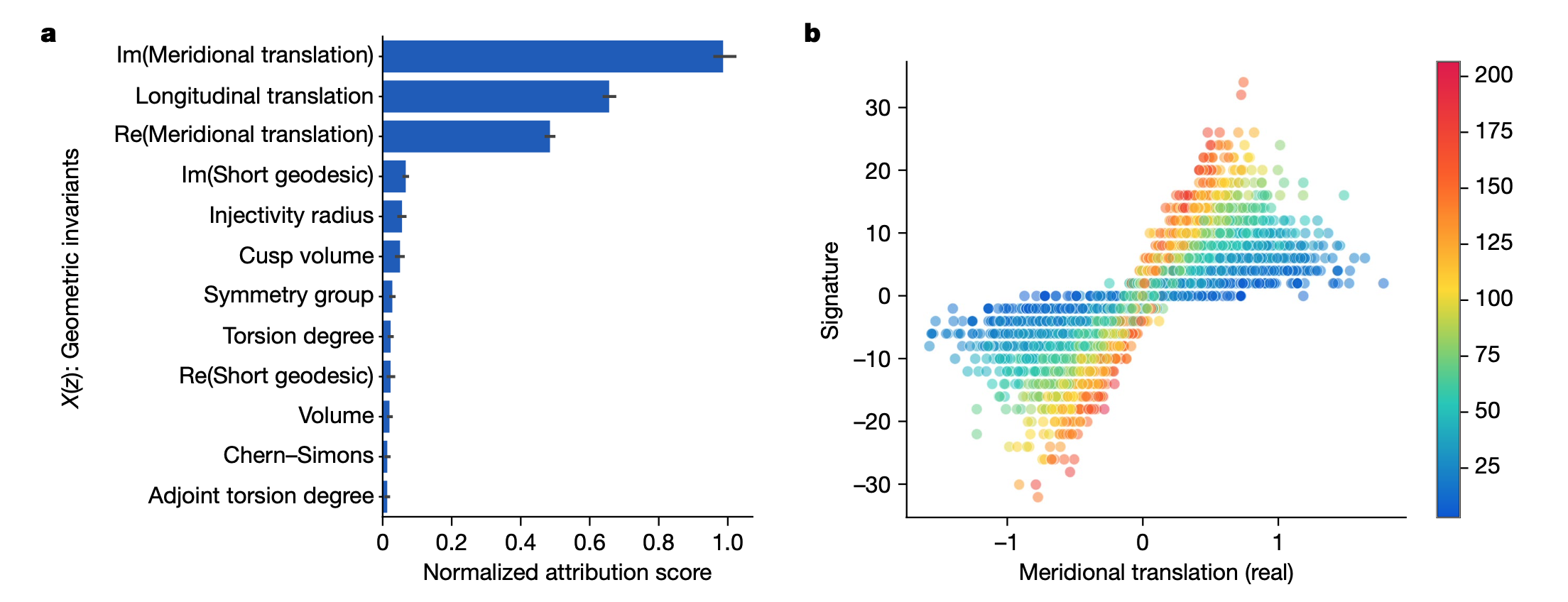
最后通过引入natural slope，slope(K) = Re(λ/μ)，meridional translation 代表 μ，the longitudinal translation 代表λ。

得出理论: 存在一个常熟c，对于任意的双曲knot K，存在不等式，|2σ(K)−slope(K)|≤cvol(K)inj(K)−3。

表示理论

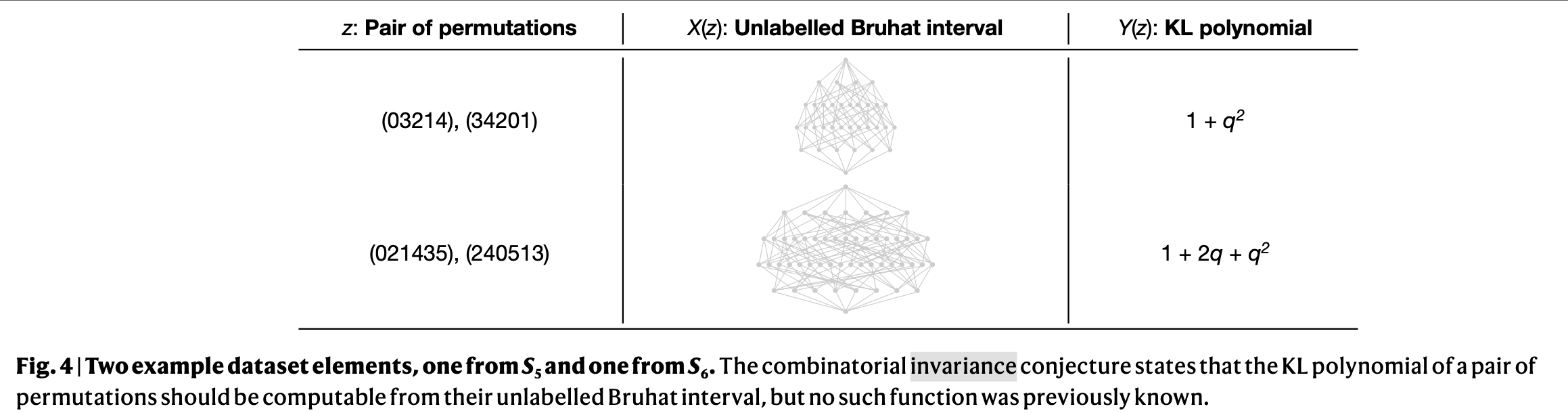
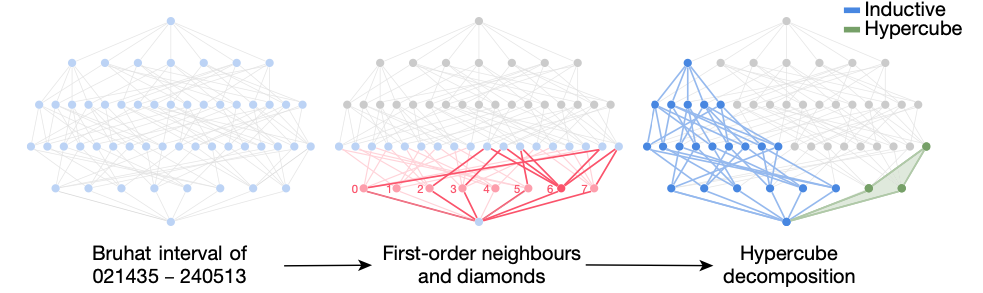
组合不变性猜想指出一对排列组合的KL多项式应该可以从其未标记的Bruhat区间中计算出来。

通过监督学习，模型可以从Bruhat区间中计算KL多项式，然后通过一系列的推理，数学家得出如下理论：

每一个Bruhat区间都有一个沿着其极值反射的典型超立方体分解，从中可以直接计算出KL多项式。

结论

抛开上述两个专业领域的数学知识，将机器学习应用于纯数学领域，为数学家提供直觉与灵感，给我们在机器智能的探索上开辟了一条道路。虽然ML只是做了一层铺垫，但是这样可以扩宽数学家的视野。对于在量化领域中使用机器学习，我也是持有同样的观点，那就是ML只是一个中间层，他帮助我们去理解和统计数据，至于从一组数据中得出一个结论，需要靠我们自身的直觉去完成，ML可以辅助我们来激发我们的直觉，所以要做量化交易，我们背后需要学习的是数学物理学理论，在数据的支撑下，通过ML来验证自己的理论猜想，从而开发出能从市场中赢利的交易模型。